LMNtalで川渡り問題を検証する

LMNtal（エレメンタル）という並行プログラミング言語があると聞き、川渡り問題の検証に使用してみました。実行にはLMNtal専用の統合開発環境LaViTを使います。

狐と鵞鳥と豆の袋（Fox, goose and bag of beans puzzle）

狐（fox）と鵞鳥（goose）と袋入りの豆（bag of beans）を持った農夫が川岸にいる。川には1艘の舟があり一方の岸から対岸へ渡ることができるが次のような制約がある。

• 農夫のみが舟をこぐことができる。
• 舟には農夫の他に1つのものしか乗せられない。
• 農夫がいないと、狐が鵞鳥を食べてしまう。
• 農夫がいないと、鵞鳥が豆を食べてしまう。

すべてを対岸に渡すにはどのような手順をとればよいか。

各岸について岸の区別（src, dst）、農夫の有無（1, 0）、狐と鵞鳥と豆の所在（fox, goose, beans）を表せるよう、初期状態を次のように記述しました。

{src, 1, fox, goose, beans}.
{dst, 0}.

次に川渡り失敗の条件をルールとして記述します。ここでは狐が鵞鳥を、鵞鳥が豆を食べてしまった場合両方についてeatenに書き換えて停止させました。

{1, $p[]}, {0, fox, goose, $q[]} :- eaten.
{1, $p[]}, {0, goose, beans, $q[]} :- eaten.

さらに川渡りのルールも加え、プログラムは次のようになります。

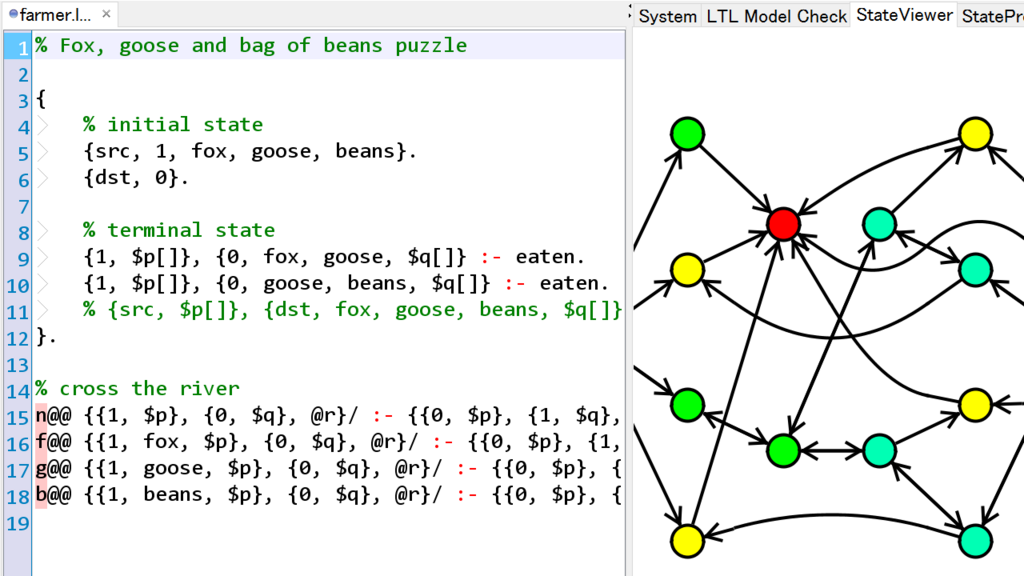
% Fox, goose and bag of beans puzzle
{
    % initial state
    {src, 1, fox, goose, beans}.
    {dst, 0}.

    % terminal state
    {1, $p[]}, {0, fox, goose, $q[]} :- eaten.
    {1, $p[]}, {0, goose, beans, $q[]} :- eaten.
    % {src, $p[]}, {dst, fox, goose, beans, $q[]} :- solved.
}.
% cross the river
n@@ {{1, $p}, {0, $q}, @r}/ :- {{0, $p}, {1, $q}, @r}.
f@@ {{1, fox, $p}, {0, $q}, @r}/ :- {{0, $p}, {1, fox, $q}, @r}.
g@@ {{1, goose, $p}, {0, $q}, @r}/ :- {{0, $p}, {1, goose, $q}, @r}.
b@@ {{1, beans, $p}, {0, $q}, @r}/ :- {{0, $p}, {1, beans, $q}, @r}.

LaViTでLMNtalプログラムを実行すると状態遷移図を表示することができます。

画像からは読み取れませんが、LaViT上でノードをクリックするとその状態を表示することができ、右から2個目にある青色のノードで川渡りが完了していると分かりました。また、赤色のノードがeatenであり停止していることも分かります。

遷移をたどることで、この川渡りが7ステップ（2通り）で可能であると確認できました。

{{dst. '0'. }, {src. '1'. fox. goose. beans. }. }.
% ↓ gooseを持って渡る
{{'1'. goose. dst. }, {src. fox. beans. '0'. }. }.
% ↓ 戻る
{{goose. dst. '0'. }, {src. '1'. fox. beans. }. }.
% ↓ foxを持って渡る
{{'1'. fox. goose. dst. }, {src. beans. '0'. }. }.
% ↓ gooseを持って戻る
{{fox. dst. '0'. }, {src. '1'. goose. beans. }. }.
% ↓ beansを持って渡る
{{'1'. fox. beans. dst. }, {src. goose. '0'. }. }.
% ↓ 戻る
{{fox. beans. dst. '0'. }, {src. '1'. goose. }. }.
% ↓ gooseを持って渡る
{{'1'. fox. goose. beans. dst. }, {src. '0'. }. }.

なお、初期状態と川渡り後の状態は対称なので逆向きにたどることもできます。

宣教師と人食い（Missionaries and cannibals problem）

3人の宣教師（missionaries）と3人の人食い（cannibals）が川岸にいる。川には1艘の舟があり一方の岸から対岸へ渡ることができるが次のような制約がある。

• すべての宣教師と人食いが舟をこぐことができる。
• 舟には2人までしか乗れない。
• いずれかの岸で人食いの数が宣教師の数より多くなると、人食いが宣教師を食べてしまう。

すべてを対岸に渡すにはどのような手順をとればよいか。

先ほどの農夫の問題と似ていますが、数に関する制約を記述するために、状態の表現方法を変えました。

{src, 1, missionaries(3), cannibals(3)}.
{dst, 0, missionaries(0), cannibals(0)}.

プログラムは次のようになりました。もっと簡潔に書けないかと悩みましたがLMNtal初心者にはこれが精一杯です。

% Missionaries and cannibals problem
{
    % initial state
    {src, 1, missionaries(3), cannibals(3)}.
    {dst, 0, missionaries(0), cannibals(0)}.

    % terminal state
    {missionaries(M), cannibals(C), $p[]}, {$q[]} :- M > 0, M < C | eaten.
    % {src, $p[]}, {dst, missionaries(3), cannibals(3), $q[]} :- solved.
}.
% cross the river
m@@
{{1, missionaries(A), $p}, {0, missionaries(B), $q}, @r}/ :-
    A >= 1, C = A - 1, D = B + 1 |
    {{0, missionaries(C), $p}, {1, missionaries(D), $q}, @r}.
mm@@
{{1, missionaries(A), $p}, {0, missionaries(B), $q}, @r}/ :-
    A >= 2, C = A - 2, D = B + 2 |
    {{0, missionaries(C), $p}, {1, missionaries(D), $q}, @r}.
c@@
{{1, cannibals(A), $p}, {0, cannibals(B), $q}, @r}/ :-
    A >= 1, C = A - 1, D = B + 1 |
    {{0, cannibals(C), $p}, {1, cannibals(D), $q}, @r}.
cc@@
{{1, cannibals(A), $p}, {0, cannibals(B), $q}, @r}/ :-
    A >= 2, C = A - 2, D = B + 2 |
    {{0, cannibals(C), $p}, {1, cannibals(D), $q}, @r}.
mc@@
{{1, missionaries(A), cannibals(U), $p}, {0, missionaries(B), cannibals(V), $q}, @r}/ :-
    A >= 1, C = A - 1, D = B + 1, U >= 1, X = U - 1, Y = V + 1 |
    {{0, missionaries(C), cannibals(X), $p}, {1, missionaries(D), cannibals(Y), $q}, @r}.

状態遷移図

右下から2個目のシアン色のノードが川渡り完了の状態です。遷移をたどることで、この川渡りが11ステップで可能であると確認できました。

まとめ

LMNtalを利用したことで直感的に記述することができました。結果をグラフィカルに表示する環境も整っているから楽しい！

LMNtalにはより複雑な機能も存在するらしくマニュアルを何度も読んでいますが未だに理解できていません。心残りなところです。